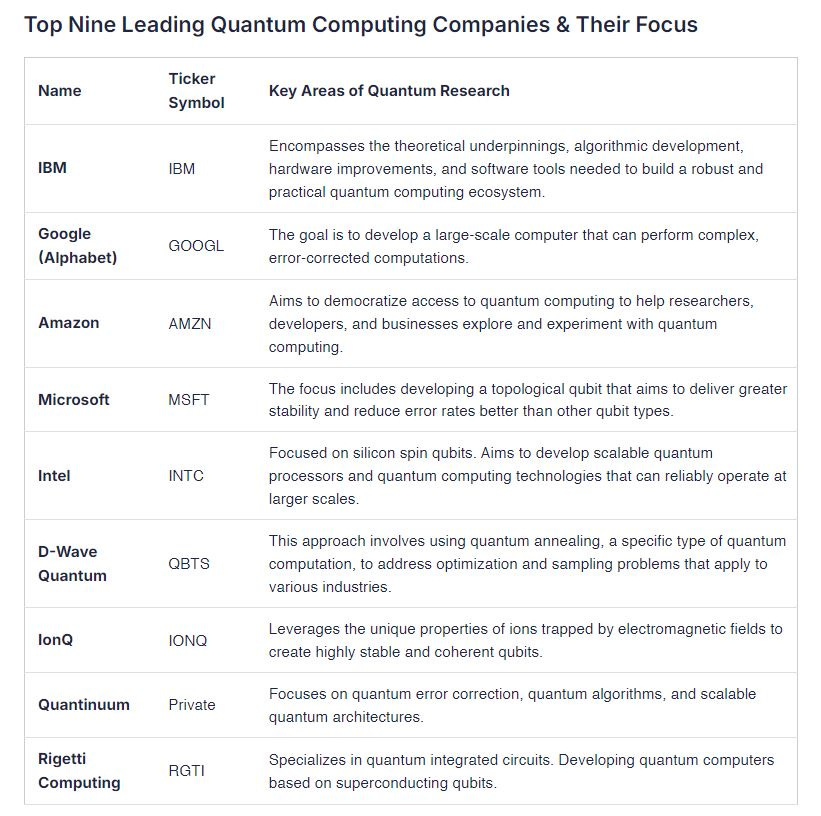
Enhancing Time Series Prediction with Quantum Machine Learning

Insights from a Quantum Variational Algorithm

Introduction

Brief overview of Quantum Machine Learning (QML) vs. traditional Machine Learning (ML)

Quantum Machine Learning (QML) and traditional Machine Learning (ML) both aim to develop algorithms that can learn from and make predictions on data, but they operate in fundamentally different computational paradigms.

Traditional Machine Learning (ML)

• Computational Basis: Operates on classical computers using bits as the basic unit of data, which can either be 0 or 1.

• Algorithms: Includes a variety of techniques such as linear regression, decision trees, neural networks, and support vector machines.

• Data Handling: ML algorithms often require substantial data preprocessing and can struggle with the curse of dimensionality in very high-dimensional spaces.

• Scalability: While ML can effectively process and analyze large datasets, the computational cost increases significantly with the complexity of models and size of the data.

• Use Cases: Widely used in applications ranging from image and speech recognition to predicting consumer behavior and financial trends.

Quantum Machine Learning (QML)

• Computational Basis: Utilizes quantum computers, which operate using quantum bits or qubits. These qubits can represent multiple states simultaneously through quantum superposition, offering a multidimensional computing space.

• Quantum Properties: Leverages quantum phenomena such as superposition, entanglement, and quantum tunneling, which can potentially provide exponential speed-ups for certain calculations.

• Algorithms: Includes quantum versions of clustering, principal component analysis, and neural networks, often using a hybrid approach that combines classical and quantum computing techniques.

• Data Efficiency: QML can theoretically handle problems with intrinsic quantum structure more naturally and efficiently, potentially reducing the dimensionality and sample complexity barriers faced by classical ML.

• Scalability and Speed: For specific types of problems, QML algorithms have the potential to outperform classical algorithms significantly, especially in factorizing large numbers (as in Shor’s algorithm) or simulating quantum systems.

Introduction to NASDAQ Time Series Prediction using Quantum Machine Learning

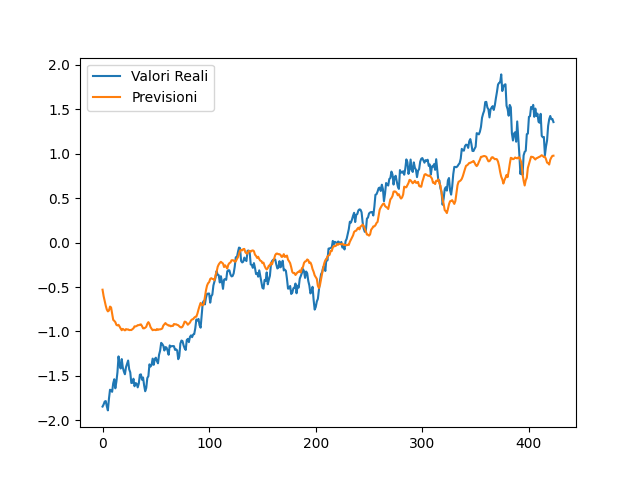
The accelerating pace of technological advancement in quantum computing has paved the way for innovative approaches to financial market predictions. This paper introduces a novel Quantum Machine Learning (QML) algorithm designed by myself specifically for predicting movements in the NASDAQ index. By leveraging the principles of quantum mechanics, this algorithm aims to provide a new lens through which financial data is analyzed, potentially surpassing traditional machine learning methods in both speed and accuracy.

Key Features of the Algorithm:

1. Data Acquisition and Preparation:

   • The algorithm begins by retrieving historical data of the NASDAQ index using the yfinance library, focusing on the comprehensive data set from January 2023 onwards.

   • Data normalization is applied to adjust the feature scale, enhancing the model’s ability to converge during training.

2. Quantum Encoding:

   • The algorithm employs angle encoding - the predominant method for encoding classical data into quantum state in QNN- where the classical data are embedded into the rotation angles of quantum rotation gates

   • to translate classical data into quantum data, preparing it for processing on a quantum circuit. This step is crucial as it maps real-valued data into angles of quantum rotations, effectively utilizing the quantum state space.

3. Quantum Circuit Design:

   • A quantum circuit is configured with rotations corresponding to the encoded angles, facilitating the entanglement and superposition properties inherent to quantum computing.

   • The Pennylane library is utilized to build and simulate the quantum circuits, allowing for the integration of quantum nodes directly within a Python environment and QISKIT code.

     

Objective:

The primary goal of this QML algorithm is to harness quantum computational power to forecast future price movements of the NASDAQ index. By applying quantum algorithms to financial time series data, it seeks to uncover patterns and dependencies not readily apparent or accessible to classical algorithms.

This approach represents a cutting-edge fusion of quantum computing and financial analysis, aiming not only to enhance predictive accuracies but also to initiate a transformative shift in how financial markets are analyzed.

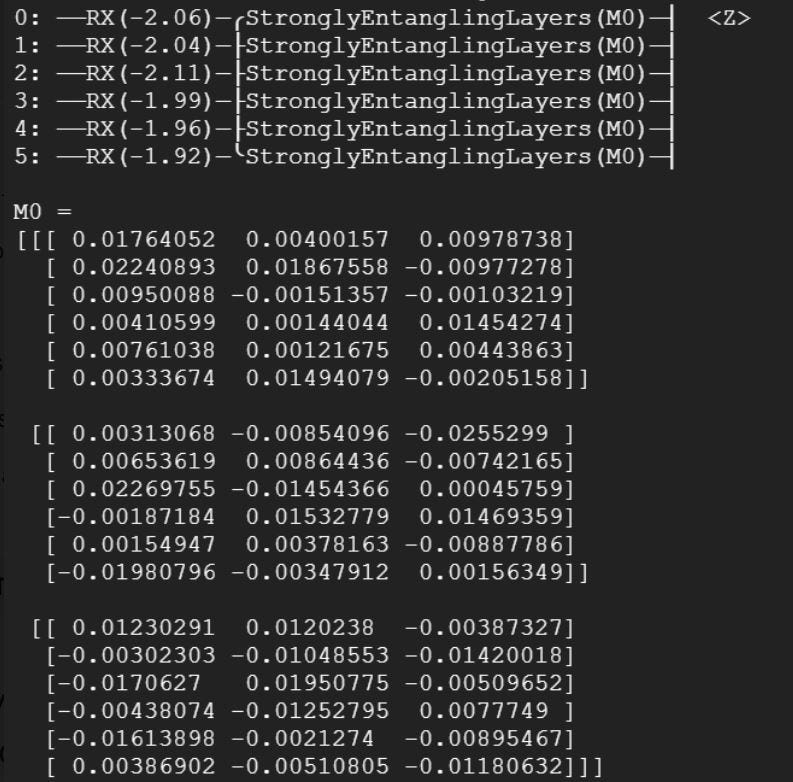
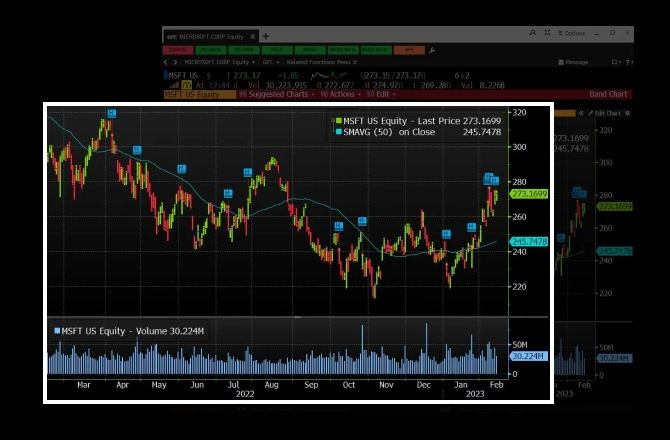
The first launch result running 50 epochs with 6 cubits and 3 quantum variational layers :

Superiority of Quantum Machine Learning Over Classical Machine Learning

Comparative Analysis

Inherent Advantages of Quantum Computing: Quantum computing introduces radical innovations in data processing through its foundational principles, which differ significantly from classical computing:

• Parallelism: Through quantum superposition, a quantum computer can represent and process multiple states simultaneously, unlike a classical computer which processes one state at a time. This allows quantum algorithms to perform many calculations in parallel, potentially leading to exponential speed-ups in data processing.

  

• Entanglement: This uniquely quantum phenomenon can link qubits in a way that the state of one (no matter how far apart they are) can depend on that of another. This enables quantum computers to perform complex problem-solving tasks more efficiently than classical counterparts, which might involve vast amounts of interdependent data.

  

Efficiency in Data Handling:

• Quantum computers can handle vast datasets by compactly encoding them into a smaller number of qubits, addressing the curse of dimensionality that often hampers classical ML. Quantum amplitude estimation and quantum Fourier transform are examples where these advantages are put into practical use, potentially reducing the complexity and computational cost of algorithms.

  

Case Studies/Research Highlights

Literature and Research:

• Studies like those conducted by researchers at Google and IBM have shown scenarios where quantum algorithms provide a clear advantage over classical algorithms, such as in the simulation of quantum materials and optimization problems.

• Quantum algorithms, like the Quantum Approximate Optimization Algorithm (QAOA) and the Variational Quantum Eigensolver (VQE), have demonstrated potential in solving complex optimization and eigenvalue problems faster than their classical counterparts.

Application in Your Algorithm:

• My NASDAQ prediction algorithm leverages quantum superposition and entanglement through its use of variational quantum circuits. By encoding data into quantum states and using entangled qubits to perform computations, the algorithm can theoretically evaluate many possible outcomes simultaneously.

• The algorithm's use of a variational approach allows it to optimize the quantum circuit parameters iteratively, which is akin to training a neural network but uses quantum mechanical effects to potentially arrive at solutions faster and more efficiently than classical methods.

Future Directions and Improvements

Enhancements in Algorithm

Increasing Accuracy and Efficiency:

• Parameter Optimization: Enhancing the variational algorithm can start with more sophisticated techniques for quantum circuit parameter optimization. Advanced optimization methods, such as quantum natural gradient, could be employed to converge more rapidly to the optimal parameters, thereby improving the algorithm’s performance.

• Error Correction Incorporation: As quantum technology matures, integrating error correction schemes into quantum algorithms will be crucial. This would mitigate the impact of quantum noise and decoherence, leading to more reliable and accurate predictions.

• Adaptive Circuit Design: Implementing adaptive quantum circuit designs that adjust the complexity of the circuit based on the problem's specific characteristics can optimize computational resources and enhance performance.

  

Expansion to Other Indices/Markets

Adaptability to Various Financial Sectors:

• Generalization: Testing and adapting the algorithm to forecast different financial indices or individual stocks could broaden its applicability. By tuning the quantum circuit to capture the nuances of various asset classes, the algorithm could be made more versatile.

  

• Global Markets: Extending the approach to global financial markets, such as emerging market indices or commodities, could provide insights into more diverse economic conditions, enhancing the robustness of the predictive capabilities.

  

Technological Advancements

Quantum Hardware Evolution:

• Scalability: Future quantum processors with more qubits and better connectivity between them will allow for more complex and larger-scale quantum computations, directly benefiting QML algorithms by providing the ability to handle more data and perform more extensive simulations.

• Coherence Time Improvement: Enhancements in qubit coherence times will permit longer computation periods before quantum information is lost, crucial for executing more extended and complex quantum algorithms.

• Commercial Quantum Cloud Services: As quantum computing resources become more widely available through cloud services, it will lower the barriers to entry for financial institutions to experiment with and deploy quantum algorithms. This democratization of quantum computing could lead to a surge in innovative financial models based on quantum technologies.

  

References

• List of academic papers, articles, and resources on SolidLedger Studio section QML on Qunatum Computing page

  

Alberto Varignana, MBA